CGAffineTransform 简单分析

AffineTransform（仿射变换）

一个任意的仿射变换都能表示为乘以一个矩阵 (线性变换) 接着再加上一个向量 (平移)。我们能够用仿射变换来表示:

旋转 (线性变换)
平移 (向量加)
缩放操作 (线性变换)

我们通常使用 2 x 3 矩阵来表示仿射变换(以下需要一些线性代数的知识)。 $A = \begin{bmatrix} a & c \\\\ b & d \\\\ \end{bmatrix}\_{2 \times 2} , \quad B = \begin{bmatrix} t\_x \\\\ t\_y \\\\ \end{bmatrix}\_{2 \times 1} \\\\ \\\\ M = \begin{bmatrix} A \\\\ B \\\\ \end{bmatrix} = \begin{bmatrix} a & c & t\_x \\\\ b & d & t\_y \\\\ \end{bmatrix}\_{2 \times 3}$

用矩阵 A 和 B 对二维向量 X 做变换，那上式也可表示为 $T = A \cdot \begin{bmatrix} x \\\\ y \\\\ \end{bmatrix} + B \quad 或 \quad T = M \cdot \begin{bmatrix} x & y & 1 \end{bmatrix}^T \\\\ \\\\ T = \begin{bmatrix} ax + cy + t\_x \\\\ bx + dy + t\_y \\\\ \end{bmatrix}$

单位矩阵，主对角线为 1，其他都为 0 的矩阵 $\begin{bmatrix} 1 & 0 & \cdots & 0 \\\\ 0 & 1 & & \vdots \\\\ \vdots & & \ddots & \vdots \\\\ 0 & \cdots & \cdots & 1 \end{bmatrix}$

CGAffineTransform 官方定义

struct CGAffineTransform {
	CGFloat a, b, c, d;
	CGFloat tx, ty;
};

虽然结构体中只有 a,b,c,d,tx,ty 6 个参数，但其实还有 3 个固定的参数[0,0,1] 来组成 3x3 的矩阵。

PS:anchorPoint 定义了应用变换的坐标系的原点。

仿射变换表示为一个 3x3 的矩阵如下: $\begin{bmatrix} a & b & 0 \\\\ c & d & 0 \\\\ t\_x & t\_y & 1 \end{bmatrix}$

对于一个 CGPoint(x, y), 经过以上仿射变换后为（x’, y’）,可表示为 $\begin{bmatrix} x' & y' & 1 \end{bmatrix} = \begin{bmatrix} x & y & 1 \end{bmatrix} \times \begin{bmatrix} a & b & 0 \\\\ c & d & 0 \\\\ t\_x & t\_y & 1 \end{bmatrix}$

即公式(1): $\label{exampleone} x’ = ax + cy + t\_x \\\\ y’ = bx + dy + t\_y$

identity 矩阵

/* The identity transform: [ 1 0 0 1 0 0 ]. */
CG_EXTERN const CGAffineTransform CGAffineTransformIdentity
  CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0);

identity 矩阵可以表示为 $\begin{bmatrix} 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1 \end{bmatrix}$ 代入公式（1），的得到 $x’ = 1x + 0y + 0 \\\\ y’ = 0x + 1y + 0$ 整理后得到 $x’ = x \\\\ y’ = y$

identity 仿射矩阵计算后的坐标也就是坐标自己本身。

CGAffineTransformMakeTranslation 方法

/* Return a transform which translates by `(tx, ty)':
     t' = [ 1 0 0 1 tx ty ] */

CG_EXTERN CGAffineTransform CGAffineTransformMakeTranslation(CGFloat tx,
  CGFloat ty) CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0);

CGAffineTransformMakeTranslation是一个进行平移的方法，根据注释得到的矩阵为 $\begin{bmatrix} 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ t\_x & t\_y & 1 \end{bmatrix}$ 代入公式（1），的得到 $x’ = 1x + 0y + t\_x \\\\ y’ = 0x + 1y + t\_y$ 整理后得到 $x’ = x + t\_x \\\\ y’ = y + t\_y$

CGAffineTransformMakeTranslation 也就是所对原来坐标进行一个平移的操作，在 x 轴方向上移动 tx，在 y 轴方向上移动 ty。

CGAffineTransformMakeScale 方法

/* Return a transform which scales by `(sx, sy)':
     t' = [ sx 0 0 sy 0 0 ] */

CG_EXTERN CGAffineTransform CGAffineTransformMakeScale(CGFloat sx, CGFloat sy)
  CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0);

CGAffineTransformMakeScale是一个进行缩放的方法，根据注释得到的矩阵为 $\begin{bmatrix} s\_x & 0 & 0 \\\\ 0 & s\_y & 0 \\\\ 0 & 0 & 1 \end{bmatrix}$ 代入公式（1），的得到 $x’ = s\_xx + 0y + 0 \\\\ y’ = 0x + s\_xy + 0$ 整理后得到 $x’ = s\_xx \\\\ y’ = s\_yy$

CGAffineTransformMakeScale 方法在x轴上缩放 sx，在 y 轴上缩放 sx

CGAffineTransformMakeRotation 方法

/* Return a transform which rotates by `angle' radians:
     t' = [ cos(angle) sin(angle) -sin(angle) cos(angle) 0 0 ] */

CG_EXTERN CGAffineTransform CGAffineTransformMakeRotation(CGFloat angle)
  CG_AVAILABLE_STARTING(__MAC_10_0, __IPHONE_2_0);

CGAffineTransformMakeRotation 是一个进行旋转的方法，根据注释得到的矩阵为 $\begin{bmatrix} \cos\alpha & \sin\alpha & 0 \\\\ -\sin\alpha & \cos\alpha & 0 \\\\ 0 & 0 & 1 \end{bmatrix}$

1、证明 x’ 和 y’ 构成圆方程

代入公式（1），的得到 $x’ = \cos\alpha x - \sin\alpha y + 0 \\\\ y’ = \sin\alpha x + \cos\alpha y + 0$ 整理后得到 $x’ = \cos\alpha x - \sin\alpha y \\\\ y’ = \sin\alpha x + \cos\alpha y$ 两边都平方，得到 $(x’)^2 = \cos^2\alpha x^2 - 2\sin\cos\alpha + \sin^2\alpha y^2 \\\\ (y’)^2 = \sin^2\alpha x^2 + 2\sin\cos\alpha + \cos^2\alpha y^2$ 两式左右都相加得到 $(x’)^2 + (y’)^2 = (\cos^2\alpha + \sin^2\alpha)x^2 + (2\sin\cos\alpha- 2\sin\cos\alpha)+ (\sin^2\alpha + \cos^2\alpha)y^2 \\\\$

化简后得到 $(x’)^2 + (y’)^2 = x^2 + y^2 = r^2$

直接就是圆的方程，这只是证明 x’ 与 y’ 在变换后任然在与 x 和 y 在以 (0,0) 为圆心的圆上。

2、真正的推导过程

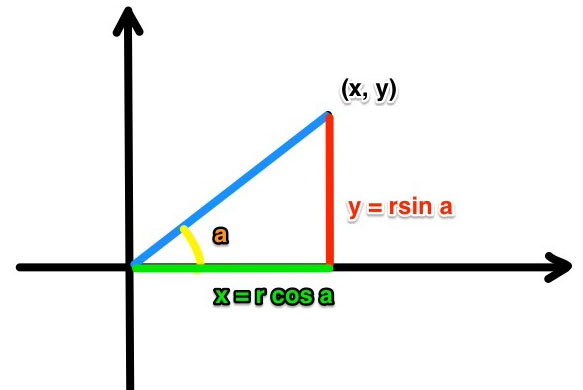
根据上图用三角函数表示公式(1) $\label{exampletwo} \begin{align} x &= r \cos \theta \\\\ y &= r \sin \theta \\\\\\\\ &逆时针旋转\alpha后\\\\\\\\ x' &= r \cos (\theta + \alpha) \\\\ &= r \cos\theta \cos\alpha - r \sin\theta \sin\alpha \\\\\\\\ &将(2)式代入 \\\\\\\\ &= \cos\alpha x - \sin\alpha y \\\\\\\\ y' &= r \sin (\theta + \alpha) \\\\ &= r \sin\theta \cos\alpha + r \cos\theta \sin\alpha \\\\\\\\ &将(2)式代入 \\\\\\\\ &= \sin\alpha x + \cos\alpha y \end{align}$

CGAffineTransformMakeRotation 方法用来计算出原来点 (x,y) 旋转 α° 之后的 (x’,y’)，即将原来的旋转 α°。也就是将 view 或者 layer 以 anchorPoint 为中心点旋转 α°

##胡乱吐槽数学真的是很奇妙的东西，矩阵虽然不明白这是如何抽象出来的，但是觉得很厉害的样子。Google 了一些资料，还是云里雾里的，只能感叹其中的精妙了。

以下摘自理解矩阵

这样的一类问题，经常让使用线性代数已经很多年的人都感到为难。就好像大人面对小孩子的刨根问底，最后总会迫不得已地说“就这样吧，到此为止”一样，面对这样的问题，很多老手们最后也只能用：“就是这么规定的，你接受并且记住就好”来搪塞。然而，这样的问题如果不能获得回答，线性代数对于我们来说就是一个粗暴的、不讲道理的、莫名其妙的规则集合，我们会感到，自己并不是在学习一门学问，而是被不由分说地“抛到”一个强制的世界中，只是在考试的皮鞭挥舞之下被迫赶路，全然无法领略其中的美妙、和谐与统一。直到多年以后，我们已经发觉这门学问如此的有用，却仍然会非常迷惑：怎么这么凑巧？

我认为，这是我们的线性代数教学中直觉性丧失的后果。上述这些涉及到“如何能”、“怎么会”的问题，仅仅通过纯粹的数学证明来回答，是不能令提问者满意的。比如，如果你通过一般的证明方法论证了矩阵分块运算确实可行，那么这并不能够让提问者的疑惑得到解决。他们真正的困惑是：矩阵分块运算为什么竟然是可行的？究竟只是凑巧，还是说这是由矩阵这种对象的某种本质所必然决定的？如果是后者，那么矩阵的这些本质是什么？只要对上述那些问题稍加考虑，我们就会发现，所有这些问题都不是单纯依靠数学证明所能够解决的。像我们的教科书那样，凡事用数学证明，最后培养出来的学生，只能熟练地使用工具，却欠缺真正意义上的理解。

自从 1930 年代法国布尔巴基学派兴起以来，数学的公理化、系统性描述已经获得巨大的成功，这使得我们接受的数学教育在严谨性上大大提高。然而数学公理化的一个备受争议的副作用，就是一般数学教育中直觉性的丧失。数学家们似乎认为直觉性与抽象性是矛盾的，因此毫不犹豫地牺牲掉前者。然而包括我本人在内的很多人都对此表示怀疑，我们不认为直觉性与抽象性一定相互矛盾，特别是在数学教育中和数学教材中，帮助学生建立直觉，有助于它们理解那些抽象的概念，进而理解数学的本质。反之，如果一味注重形式上的严格性，学生就好像被迫进行钻火圈表演的小白鼠一样，变成枯燥的规则的奴隶。。

-以上-